EL UNIVERSO MECÁNICO: VOLTAJE, ENERGÍA Y FUERZA

 

No nos engañemos. El concepto de voltaje no es sencillo. Pero este extraordinario vídeo de la colección El Universo Mecánico puede ayudarnos sin duda a obtener una visión más intuitiva del mismo. Atención al símil entre campo eléctrico y campo gravitatoria para que podamos imaginarnos mejor el concepto de voltaje.

CALCULAR EL CAMPO ELÉCTRICO EN UN PUNTO

Aquí tenéis varios vídeos con ejercicios en los que se indica, paso a paso, cómo calcular el campo eléctrico en un punto.

REACCIONES BÁSICAS DE DESINTEGRACIÓN NUCLEAR

Las reacciones básicas de desintegración nuclear suelen producirse en elementos de la tabla periódica de elevado número atómica. Muchos de estos elementos pertenecen a los grupos de los lantánidos, actínidos o tierras raras. Para sacar el balance de la reacción hay que identificar el tipo de emisión radioactiva que se ha producido y asegurarse que se conserva la carga eléctrica y el número atómico, buscando a través de ello determinar cuál es el nuevo elemento químico que se ha generado por transmutación.

En esta versión de la tabla periódica podemos apreciar el nivel de radioactividad según un código de colores indicado en la misma.

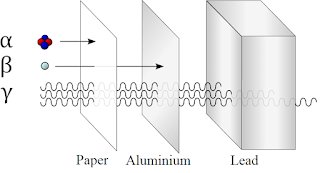
Dependiendo del tipo de emisión producida varía enormemente la longitud de penetración de la misma.

LOS 3 TIPOS DE EMISIÓN RADIOACTIVA

El descubrimiento de la radioactividad pudo de manifiesto que a nivel subatómico ciertos procesos desconocidos acontecían en determinados materiales. Al tiempo se vio que estos procesos tenían lugar en el interior del núcleo atómico y que, según su naturaleza, podían dar pie a tres tipos diferentes de radiación:

• Radiación alfa: debida a la emisión de núcleos de helio, con una doble carga positiva (tienen dos protones y dos neutrones en su interior), más masivos, altamente ionizantes del medio que atraviesan y que se desvían hacia la derecha al atravesar un campo magnético.
• Radiación beta: debida a la emisión de partículas cargadas negativamente, menos ionizantes que la radiación alfa y que se desvían hacia la izquierda ante la presencia de un campo magnético, las cuales se acabaron asociando con simples electrones.
• Radiación gamma: radiación electromagnética de muy corta longitud de onda (alta frecuencia), neutra y, por lo tanto, que no se desvía ante la presencia de un campo magnético. La menos ionizante de todas.

Las dos primeras formas de radiación fueron descubiertas por Rutherford; la tercera por Paul Villard. 

RADIOACTIVIDAD

La radioactividad fue descubierta por Becquerel, si bien en gran parte como fruto de un suceso accidental. Becquerel se limitó a tirar del hilo del hallazgo realizado por Röngten, quien observó la manifestación de un efecto fluorescente sobre determinados materiales debido a un cierto nuevo tipo de radiación que provenía de un tubo de rayos catódicos.

El propósito de Becquerel fue el de estudiar directamente las propiedades de materiales que muestran cierto grado de fluorescencia natural. En esa época la fotografía había empezado a dar sus primeros pasos y Becquerel era un apasionado aficionado a la misma, hecho que aprovechó para realizar ciertas experiencias científicas en las que involucraría uno de estos materiales fluorescentes. Lo que hizo fue envolver una placa fotográfica con papel negro, colocó una moneda encima y la cubrió con un material que contenía uranio. Pero Becquerel pensaba que la luz solar era necesaria para que la moneda quedara impresa en la placa fotográfica. Así que realizaba sus experiencias durante el día. Y efectivamente la moneda quedaba impresa. El hecho inesperado sucedió un día que estaba nublado. Sin expectativas de poder realizar la experiencia ese día, guardó todo el "pack" en un cajón de escritorio. Al día siguiente, ante su sorpresa, comprobó como la moneda también se había impreso y, de hecho, con muchísima mayor intensidad. Este hecho puso de manifiesto que la existencia de una radiación, hasta entonces desconocida, procedente exclusivamente del mineral de uranio.

Tras el descubrimiento de la radioactividad por parte de Becquerel, fueron Pierre y Marie Curie quienes más se adentraron en esta nueva rama de la física, trabajando minuciosamente como un verdadero equipo para identificar y analizar nuevos materiales radioactivos, sus propiedades, como el el nivel de actividad por unidad de sustancia. Gracias a ello, Marie Curie fue la primera mujer de la historia en ganar, junto a su marido, el premio nobel de Física. Al año siguiente además, ganaría en solitario el premio nobel de Química. Aunque a la postre pagaría un altísimo precio por ello. No conscientes todavía del poder dañino de la radioactividad en dosis no controladas sobre el organismo, los estudios experimentales que realizó a durante largos años, en los que utilizó sobretodo toneladas de pechblenda, provocaron su muerte prematura por cáncer.

Y sin embargo, ya desde lo años 30/40, el uso limitado de los efectos radioactivos de ciertas sustancias fue introducido en la medicina con fines terapéuticos. Su efecto en la detección e incluso combativo de tumores cancerígenos frente al influjo negativo pasaba a ser una cuestión de dosis, tiempos de exposición y localización. Todo ello ha ido evolucionando hasta hoy en día dando lugar a las diferentes técnicas modernas de la medicina nuclear.

LA CÁMARA FOTOGRÁFICA

La cámara fotográfica es uno de los instrumentos ópticos más extendidos entre la población a día de hoy. Podemos decir que los padres de la cámara de fotos son la Óptica y la Química, aunque en tiempos más recientes debemos añadir sin duda la Electrónica y la Informática entre sus constituyentes también.

La cámara fotográfica surge gracias a la combinación de diversos hitos y descubrimientos tras largos siglos de investigación sobre la base de una invento primigenio: la cámara oscura.

Merece la pena de ver el vídeo de arriba para hacerse una idea intuitiva pero bastante completa de cómo funciona una cámara de fotos actual y cómo operan los principales componentes que la integran.

EL TELESCOPIO

El precursor del telescopio fue el anteojo astronómico, compuesto por dos lentes convergentes dispuestas de forma que el foco imagen de la primera coincidiera con el foco objeto de la segunda. Su principal inconvenientes es que creaba una imagen muy aumentada, pero invertida.

Esto lo resolvió Galileo con sistema compuesto por una lente convergente y otra divergente. Además, el anteojo de Galileo reduce considerablemente la longitud del mismo.

El siguiente prototipo inventado fue el telescopio de Newton y se basaba en espejos; una idea sencilla, pero poderosa, aunque tenía el inconveniente de dejar una zona muerta en el centro que no se podía cubrir.

Otro diseño parecido fue el correspondiente al telescopio de Cassegrain:

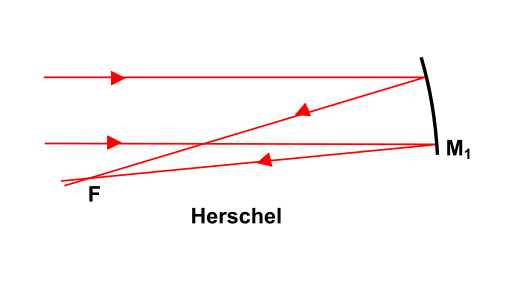
El problema de la zona media no cubierta se resolvía con el telescopio de Herschel, aunque a cambio de una ligera asimetría en el trazado de rayos.

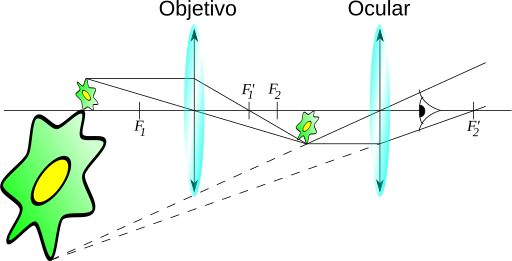
EL MICROSCOPIO

El microscopio es un sistema óptico compuesto por dos lentes ópticas llamadas objetivo y ocular que se combinan apropiadamente para que el ojo observe una imagen aumentada (virtual e invertida). Fue inventado por Robert Hooke y con él pudo ver las primeras células (muertas), las cuáles dibujó.

LA LUPA

Podemos decir que la lupa es el instrumento óptico más sencillo que existe. En realidad se trata de una simple lente convergente con una distancia focal apropiada para aumentar el tamaño de los objetos observados. Normalmente la lupa se utiliza para observar objetos colocados entre el punto próximo y el ojo humano. El punto próximo se corresponde con aquella distancia mínima a la que el ojo humano puede enfocar objetos con nitidez y suele ser de unos 25 cm. Lo ideal es que el objeto caiga exactamente sobre el foco de la lupa para poderlo ver con vista relajada (como si los rayos provinieran paralelos del infinito). En tal configuración el observador obtendrá una imagen virtual y le parecerá que los rayos de luz le llegan con un mayor ángulo de incidencia que el real.

Es precisamente el aumento angular lo que se tiene en cuenta para determinar la capacidad de aumento de una lupa. Este aumento angular se define como el cociente entre las tangentes del ángulo subtenido por los rayos de luz que provienen del objeto con y sin la lupa.

Considerando el objeto precisamente colocado sobre el punto focal cuando se utiliza la lupa frente al ángulo máximo del objeto que se observará sin lupa cuando se coloca justo en el punto próximo obtendremos un aumento lateral de 

Sin embargo la distancia focal no se puede reducir infinitamente ya que eso requeriría lentes de un radio de curvatura cada vez menor y la aberración esférica aparecería imponiendo límites prácticos.

DEFECTOS DE LA VISIÓN

Los dos principales defectos de la visión son:

• miopía: cuando la imagen se crea siempre antes de la retina (más allá del límite de acomodación del ojo). Se corrige anteponiendo al ojo una lente concava de forma que la distancia focal del sistema óptico compuesto se aleje hasta llegar a la retina. Este defecto se produce cuando el ojo es más largo de lo normal, motivo por el que la distancia focal se queda demasiado "corta".
• hipermetropía: cuando la imagen se crearía de forma nítida más allá de la retina (por más que uno se acerque al límite de acomodación del ojo). Se corrige anteponiendo al ojo una lente convexa de forma que la distancia focal del sistema óptico compuesto se acerque hasta llegar a la retina. Este defecto se produce cuando el ojo es más corto de lo normal, motivo por el que la distancia focal resulta demasiado grande.
• plesbicia o vista cansada: reducción de la capacidad de acomodación debida a la fatiga de los músculos ciliares o a la pérdida de flexibilidad del cristalino.
• astigmatismo: debido a la falta de esfericidad perfecta del ojo. Dificulta la visión clara y simultanea de dos rectas perpendiculares, de los radios de la rueda de una bicicleta...

• cataratas: pérdida de transparencia del cristalino.
• daltonismo: dificultad de distinguir determinados colores; confusión del rojo por el verde. Relacionado con la ausencia o deficiencia de determinados conos de la retina.

FOTO-RECEPCIÓN DEL OJO HUMANO: CONOS Y BASTONES

Los bastones son el tipo de célula neuronal que indica el nivel de intensidad lumínica que entra al ojo (relación luz/oscuridad).

Los conos son el tipo de célula neuronal capaz de discriminar entre los tres tipos de colores primarios asociados a la imagen que se proyecta en la retina, dependiendo de la longitud de onda asociada a cada uno de sus fotones.

EL OJO HUMANO

El ojo está constituido por un sistema óptico basado en una lente biconvexa (cristalino) de distancias focal variable (acomodación).

PATRONES DE DIFRACCIÓN

El fenómeno de la difracción se produce cuando un frente de ondas se encuentra con un obstáculo o una rendija en su camino. El efecto de este fenómeno ondulatorio es la emergencia de unos patrones de difracción que ponen de manifiesto la aparición de zonas donde se producen máximos de intensidad más allá de lo que uno podría esperar por la alineación del foco emisor con la rendija.

La primera teoría que consiguió explicar este fenómeno se conoce como principio de Huygens, que consiste básicamente en considerar cada uno del los puntos del espacio localizados en la zona de la rendija como fuentes emisores secundarias de la misma frecuencia que la onda incidente. De forma que la aplicación del principio de superposición a las ondas generadas por tales emisores secundarios dará lugar a un fenómeno de interferencia conjunta que deriva en los susodichos patrones de difracción.

Para la obtención de las expresiones matemáticas exactas que describen los patrones de difracción de una rendija rectangular o circular es preciso cierto dominio de cálculo de integrales definidas o en su defecto la aplicación de transformadas de Fourier.

Los patrones de difracción han sido una valiosísima herramienta para el descubrimiento experimental de importantísimos hitos científicos, como son la naturaleza ondulatoria de la luz, la confirmación de la naturaleza ondulatoria de las partículas constituyentes de la materia o la determinación de la estructura en doble hélice de la molécula de la vida, el ADN.

REFLEXIÓN Y REFRACCIÓN SEGÚN EL PRINCIPIO DE HUYGENS

Tanto el fenómeno de la reflexión como el de la refracción de una onda pueden explicarse a partir del principio de Huygens.

Por ejemplo, en el caso de la reflexión, podemos imaginar dos rayos paralelos que llegan con cierto ángulo a una superficie limítrofe. Dado que ambos viajan a la misma velocidad, uno llegará antes que el otro, al estar inclinados. Hay que imaginarse que el punto al que llegue el primero actuará antes como un foco emisor secundario. Cuando llegue el segundo rayo al punto de reflexión, el frente de onda reflejado emitido por el primer emisor secundario ya estará a cierta distancia. Si consideramos cualquier otro rayo entre ambos y la posición de todos los frentes de onda reflejados, y los alineamos en un instante dado, triangulando se pone de manifiesto que los rayos reflejados salen con la misma inclinación respecto a la normal que el ángulo incidente.

En el caso de la refracción, lo que ocurre es que el frente de ondas refractado emitido por el primer punto que actúa como emisor secundario en la superficie de separación entre los dos medios viaja a una velocidad diferente, supongamos menor. Esto implica que cuando alcance la superficie de separación el rayo paralelo más alejado del primero, la distancia recorrida por el frente de ondas referido será menor que la que, en el mismo tiempo, ha recorrido éste en el primer medio. De lo que resulta por triangulación, que los frentes de ondas al viajar más despacio se desvían respecto al haz incidente con un ángulo menor respecto a la normal. La relación que se obtiene por triangulación entre los ángulos incidente y refractado y las velocidades respectivas de propagación o, lo que es lo mismo, los índices de refracción en cada medio, coincide con la Ley de Snell.

EFECTOS DEL PRINCIPIO DE HUYGENS

Tal y cómo puede apreciarse en este vídeo, una de las consecuencias más sorprendentes del principio de Huygens es que un frente de ondas pueda atravesar una serie de obstáculos con rendijas no alineadas y llegar al otro lado.

PRINCIPIO DE HUYGENS

El principio de Huygens arroja una visión de los frentes de onda que permite explicar de forma intuitiva diferentes fenómenos ondulatorios como lo son la reflexión, la refracción y la difracción de ondas.

Esencialmente Huygens concibió los frentes de ondas como zonas del espacio en las que cada punto se comportaba a su vez como un emisor de ondas secundario, de suerte que las ondas re-emitidas tendrían la misma frecuencia y longitud de onda (por lo tanto la misma velocidad), aunque menos amplitud en virtud de la disminución de la misma con la distancia.

Lo que comúnmente ocurre es que las ondas producidas por estos focos secundarios, que se corresponden con todos los puntos de un mismo frente de ondas, interfieren de tal manera que solamente se produce una interferencia constructiva para todos los puntos que se corresponden con posteriores frentes de ondas. En cualquier otro punto, la interferencia de las ondas provenientes de todos esos puntos es destructiva, dando como resultado una intensidad nula.

Eso es lo que sucede en el espacio abierto. Pero cuando lo que ocurre es que la onda se encuentra con un obstáculo, una parte se refleja y otra se refracta. Y cuando se encuentra con una abertura o rendija en medio de un obstáculo, entonces se produce un patrón de difracción.

El patrón de difracción solamente es apreciable cuando la longitud de la rendija es comparable con la longitud de onda de la onda incidente y puede explicarse de forma descriptiva aplicando el principio de Huygens.

ANÁLISIS DEL FOURIER

Cuando nos disponemos a estudiar los fenómenos ondulatorios damos con el hecho de que hay un tipo de onda que podemos etiquetar como 'ideal'. Esta es la onda sinusoidal. La función matemática que la describe ofrece la solución más sencilla a la ecuación diferencial de una onda. Pero no la única...

De hecho, cuando escuchamos la misma nota musical proveniente de una guitarra eléctrica o de una flauta, ¿qué es lo que las distingue? Si ambos tonos se correspondieran únicamente con una única función sinusoidal, sonarían igual...

El matemático francés Jean Baptiste Fourier ideó a principios del siglo XIX un mecanismo a través el cual cualquier función periódica, sea cual sea su forma, puede ser descompuesta en una suma infinita de funciones sinusoidales. A este desarrollo se le conoce como serie de Fourier.

En la serie (finita o infinita) de Fourier, al término que se corresponde con la frecuencia más baja se le denomina fundamental y normalmente es el que tiene una amplitud o contribución mayor. A partir de ahí aparecen otros términos cuyas frecuencias son múltiplos directos de la fundamental y que se conocen como armónicos. Normalmente, conforme va aumentando la frecuencia de los armónicos de una serie de Fourier, su peso o contribución al sumatorio total, es cada vez menor.

Tanto el tono de la guitarra como el de la flauta tienen la misma frecuencia fundamental, pero se distinguen en el número de armónicos y su intensidad.

Una forma alternativa de visualizar una onda es precisamente desde el punto de vista frecuencial; es decir, representando en un gráfico la intensidad de su frecuencia fundamental y todos sus armónicos. A esta representación se la conoce como espectro de frecuencias y en la actualidad puede verse utilizando un equipo electrónico (un poco caro, por cierto) que se conoce como analizador de espectros.

Si se hace tender el periodo de la función periódica cuya serie de Fourier se pretende obtener a infinito (con lo cual deja de ser periódica) entonces la serie deja de tener una representación de valores discretos (múltiplos de la frecuencia fundamental) y se torna continua, normalmente quedando delimitada a un rango de frecuencias. Esto se conoce como transformada de Fourier.

EFECTO DOPPLER

Todo el mundo conoce por experiencia propia que cuando una ambulancia se acerca a nosotros y luego pasa alejándose, cambio de forma notable el tono que percibimos de la sirena. Esto es debido al efecto Doppler.

Es importante subrayar que las ondas de sonido son ondas mecánicas, lo que implica que necesitan un medio físico para propagarse (no así las ondas electromagnéticas). Es por eso que el sonido no puede propagarse en el vacío...

Cuando la ambulancia se acerca a nosotros, desde nuestro punto de vista, es cómo si ésta persiguiera al propio sonido que emite. Simplifiquemos un poquito las cosas para hacerlas más manejables suponiendo que el sonido que emite es un tono puro. O sea, que tiene una frecuencia única y bien definida. Esa onda de sonido viaja con la velocidad del sonido en el aire hacia todas direcciones. Pero en la dirección que va de la ambulancia a nosotros, el foco emisor se acerca a los frentes de onda con la velocidad de la propia ambulancia. El efecto práctico de esto es que los frentes de onda se comprimen, por lo que la longitud de onda que nosotros percibimos se hace más corta. La frecuencia, por lo tanto, se vuelve más aguda.

Si la ambulancia se alejara de nosotros, como es lógico, sucedería lo contrario; la longitud de onda se haría mayor, con lo que escucharíamos un sonido más grave (no hay más que cambiar el signo de la velocidad de la ambulancia en la expresión de arriba para llegar rápidamente a esta conclusión).

La forma más general de considerar el efecto Doppler es cuando tanto el emisor como el receptor se mueven con velocidades constantes dadas, ya sea en el mismo u opuesto sentidos (lo cuál no es más que una cuestión de signos). En tal caso la frecuencia que percibirá el receptor será:

Para un uso práctico de la expresión que da cuenta de la frecuencia que percibe el receptor, lo ideal es utilizarla para el caso más general y ser muy cuidadoso a la hora de aplicar bien el criterio de signos a todas las velocidades. Es tan simple cómo, sustituir como positivas todas las velocidades que se mueven hacia la derecha, negativas todas las que van hacia la izquierda, y nulas las que se corresponden a emisor o receptor que no se mueve.

El efecto Doppler fue estudiado y enunciado por un científico austríaco al que se le debe el nombre y adquirió especial relevancia dentro de la Historia de la Física por su aplicación en el experimento de Micherson-Morley, experimento cuyos inesperados resultados llevarían a la formulación de la Teoría de la Relatividad (primero Espacial y más adelante General).

ONDAS DE SONIDO

El sonido es un caso particular de onda que se propaga por el espacio debido a un cambio de presión que se traslada provocando pequeñas oscilaciones en la densidad el medio por el movimiento de las moléculas del mismo, con la particularidad de que lo podemos oír. Como toda onda, el sonido se caracteriza por su intensidad y su tono (y su timbre). La intensidad depende de la amplitud y el tono de la frecuencia. El timbre depende del número de ondas armónicas que se superponen. Es lo que distingue la "personalidad" de los diferentes instrumentos de una orquesta.

ECUACIÓN DE UNA ONDA ESTACIONARIA

Lo único que hay que hacer para obtener la ecuación de una onda estacionaria es aplicar el principio de superposición con la onda incidente y la reflejada, el valor de cuyos parámetros es exactamente el mismo, sólo distinguiéndose por el signo que pone de relieve la dirección en la que se propagan:

• + hacia la izquierda
• - hacia la derecha

Lo que se obtiene es un valor de la amplitud que depende de la posición oscilando según un término temporal que depende de la frecuencia. Tal amplitud muestra unos valores máximos (vientres) y nulos (nodos) para ciertas posiciones en función del número de onda.

ONDAS ESTACIONARIAS Y RESONANCIA

La intensidad del sonido en el interior de un tubo de Kundt alcanzará máximos y mínimos en diferentes puntos dependiendo de la frecuencia del tono inyectado en el mismo y de la longitud del medio en el que se propaga antes de reflejarse. Esta longitud se puede ajustar utilizando un émbolo móvil.

Esto puede utilizarse como técnica, basada en le percepción auditiva para detectar los puntos en los que se encuentran los vientres y los nodos para cada frecuencia, y de ahí deducir la velocidad de propagación del sonido igual que se puede hacer con bolitas de porexpan.

La onda de intensidad oscila entre un máximo de amplitud 2A y 0, mientras la onda incidente y la reflejada oscilan entre -A y A.

ONDAS ESTACIONARIAS EN UN CÍRCULO

Este vídeo es muy interesante porque muestra como se crean ondas estacionarias en un círculo. Esto es lo que propuso el modelo atómico de Bohr que le pasaría al electrón alrededor del átomo, lo que conllevó la postulación del primer principio de cuantización atómica.  Por lo tanto, esta es la piedra angular sobre la que nació la Física Cuántica.

Como se puede apreciar en el vídeo solamente puede existir un número discreto de valores de longitudes de onda que mantengan ondas estacionarias en un círculo. La consecuencia inmediata de ello a nivel atómico es que el electrón tiene que ser una onda!!!

PRINCIPIO DE SUPERPOSICIÓN, ONDAS ESTACIONARIAS Y FÍSICA CUÁNTICA

Hasta ahora hemos visto como se comporta y caracteriza una onda armónica. ¿Pero cómo podemos describir lo que sucede cuando varias ondas viajan por el mismo medio? Eso viene dado por el principio de superposición.

El origen estricto del principio de superposición es puramente matemático y requiere que un sistema o fenómeno físico pueda ser descrito por un sistema de ecuaciones diferenciales lineales. Una manera simplificada de ejemplificar tal tipo de ecuaciones es imaginar una función y(x). La función es lineal si la solución suma de las soluciones que se obtienen a partir de dos valores diferentes de x, 

y1 + y2 = f(x1) + f(x2) 

es igual a la solución que se obtiene directamente de la suma de los dos valores de x,

y12 = f(x1 + x2)

y1 + y2 = y12

La consecuencia de ella es que, aplicado a las ondas, cada onda se comporta como si las demás ondas no estuvieran presentes en el medio.

Si uno quiere hallar el comportamiento total de todas las ondas que se propagan en un medio, puede hallar la ecuación que describe a cada una de ellas y no debe hacer más que sumarlas todas para hallar la ecuación final que las describe a todas a la vez.

Uno de los casos específicos en lo que se aplica el principio de superposición es el de la ondas estacionarias. Estas son ondas que se producen en un medio que esta fijo por uno o ambos extremos; como puede ser una cuerda. Lo que ocurre es que por el extremo que está fijo el medio de propagación, al llegar una onda, es reflejada. Entonces, al haber una onda incidente y otra reflejada, la onda total resulta de la superposición de ambas.

Un caso aún más específico se da cuando una onda estacionaria se produce en un círculo. 

En todos los casos las ondas estacionarias ponen de relieve que éstas solamente pueden perdurar si su longitud de onda guarda una relación concreta con la longitud entre los extremos o del círculo. Es decir, que las ondas estacionarias solamente existen para un número discreto de longitudes de ondas.

Esto es lo que llevaría a la formulación del primer principio de cuantización que daría nacimiento a la Física Cuántica. 

Siendo rigurosos, el principio de superposición solamente es válido para las ondas electromagnéticas y ondas mecánicas de pequeña amplitud, como las ondas sonoras. Para ondas mecánicas de gran amplitud, las vibraciones locales del medio ya no pueden ser descritas como osciladores armónicos y las ecuaciones reales que las modelan incluyen términos no lineales como senos y cosenos. 

ONDAS ESTACIONARIAS

Las ondas estacionarias se producen cuando una onda viaja en un medio hasta un punto en el que es reflejada, de suerte que la onda incidente y la reflejada interfieren de tal forma que se crea un patrón fijo en el espacio de puntos donde hay máximos y mínimos. Los máximos se dan donde la interferencia es siempre constructiva y los puntos en los que se producen se denominan vientres. Los mínimo se dan donde la interferencia es siempre destructiva y los puntos en los que se producen se denominan nodos. En los nodos la amplitud de la onda es nula.

La condición sin-ecuanum para que haya ondas estacionarias es una relación geométrica entre la longitud de onda y la distancia entre el punto donde se generan las ondas y el punto en el que se reflejan. El resultado de esta condición es una serie de valores discretos de longitudes de onda. Cualquier longitud de onda que verifique esta condición dará pie a ondas estacionarias. Esto conduce a que variando la frecuencia de la perturbación que genera las ondas encontremos ciertos valores para los que éstas sean estacionarias.

Hay dos escenarios generales en los que se pueden producir ondas estacionarias. El primero es aquel en el que los dos extremos del medio de propagación se corresponden con un nodo. El más claro ejemplo de ello es una cuerda fija por los dos extremos. Este es el caso que vemos en el vídeo que acompaña a esta entrada. El segundo escenario es aquel en el que el medio de propagación presenta en un extremos un nodo y en el otro un vientre. Un ejemplo es un tubo que tiene una superficie límite por un extremo pero está abierto por el otro.

Dependiendo de si consideramos un medio con los dos extremos fijos o un extremo abierto la relación entre la longitud de onda y la longitud total para que se produzcan ondas estacionarias cambiará.

Las ondas estacionarias son las que están detrás de la reverberación que genera los sonidos característicos de los instrumentos musicales. También son imprescindibles para comprender el principio que daría pie a la primera cuantización de la Física Cuántica.

ECUACIÓN DE UNA ONDA ARMÓNICA

Una onda no es otra cosa que la propagación de una perturbación. Cuando la perturbación es periódica y actúa de forma que su dependencia con el tiempo es sinusoidal, la ecuación de la onda puede hallarse como la traslación del movimiento armónico simple al que está sometido cada punto del medio afectado por la onda.

Cuando en la expresión final tenemos un signo negativo entre el término temporal y el espacial, se conviene que la onda se propaga hacia la derecha. Cuando lleva un signo positivo, la onda se propaga hacia la izquierda.

La onda se caracteriza por:

• Amplitud A
• Frecuencia ?(omega).
• Número de ondas k

MOVIMIENTO ARMÓNICO SIMPLE

El movimiento que genera una onda periódica es consecuencia del transporte de la energía de la perturbación que la ha originado en una determinada dirección.  Pero al nivel de un punto concreto del medio en el que se propaga la onda, el tipo de movimiento que ese punto experimenta es un movimiento armónico simple.

En esencia, un movimiento armónico simple es el que experimenta un objeto a cuenta de una fuerza recuperadora elástica que actúa para volverlo a llevar a su posición de equilibrio después de que una fuerza externa lo haya alejado del mismo.

El caso más sencillo de movimiento armónico simple es el del muelle elástico, el cual se caracteriza por su constante de recuperación elástica k y la masa del cuerpo m que pende de él. La fuerza recuperadora elástica es descrita por la Ley de Hooke. El análisis de todas las fuerzas operando en el sistema conduce a la ecuación diferencial que, resulta, lo describe como un sistema oscilante cuya frecuencia depende, como se ve en el vídeo, de k y de m.

Sin duda lo más interesante es que para el movimiento armónico simple el periodo de las oscilaciones sea constante, ya que depende únicamente de las propiedades del sistema, y no de su amplitud. De forma que, aunque debido a las pérdidas por rozamiento la amplitud de las oscilaciones vaya disminuyendo, cada oscilación durará exactamente igual. Ese valor, para el muelle elástico, depende únicamente de k y de m. ¿Ocurrirá lo propio con un péndulo simple?

ONDAS LONGITUDINALES Y TRANSVERSALES

En las ondas transversales las oscilaciones se producen en un eje perpendicular a la dirección de propagación.

En las ondas longitudinales las oscilaciones se producen en la misma dirección que la propagación.

En ambos casos lo que se transmite es energía, pero no materia.

ONDAS PLANAS

El estudio de las ondas se centra muy a menudo en un caso práctico conocido como ondas planas. Las ondas planas no existen realmente ya que todas las ondas deben partir de un foco emisor y, por lo tanto, sus frentes de onda tienen que mostrar convergencia hacia un punto. Para ondas planas, el foco emisor se encontraría en el infinito.

Si las ondas fueran generadas por un foco puntual, los frentes de onda serían superficies esféricas. Pero en realidad los focos emisores tienen una forma dada y ocupan un espacio, como ocurre con una antena emisora de radio, por ejemplo, y entonces la forma de los frentes de onda se puede complicar bastante.

Sin embargo, a grandes distancias, es más que aceptable asemejar el foco emisor a un punto, y aproximar las ondas esféricas a ondas planas, ya que si comparamos las superficies concéntricas de esferas muy grandes en una escala muy pequeña respecto a su radio, éstas parecen planos paralelos.

En esta aproximación, las ondas pueden ser descritas por una ecuación que solamente dependerá de una variable espacial y el tiempo. De lo contrario, la posición en la ecuación de onda debería ser tratada con un vector r = (x, y, z). De igual manera,  fuera de la aproximación de ondas planas, el número de ondas k, se tendrá que tratar como un vector de componentes k = (kx,ky,kz).

En el vídeo de abajo podemos ver los frentes de onda de ondas planas generadas en este caso con una cubeta de ondas, sin necesidad de recurrir, por lo tanto, a la aproximación mencionada anteriormente.

ONDAS

Tras haber visto, con todo lujo de detalles, cómo se predijo y posteriormente se demostró la existencia de las ondas electromagnéticas, ha llegado el momento de dirigir nuestro estudio a los que son las ondas en sí, sus características, sus propiedades y su formulación.

Sirvan este par de vídeos de la colección "El Universo Mecánico" para abrir esta sección.

MÁQUINA DE ONDAS

En una máquina de ondas hecha con fines didácticos podemos apreciar como se propaga la perturbación a través de una onda. Aunque la forma más fácil de imaginarnos y representar una onda es cuando ésta oscila en una sola dirección, muy a menudo el movimiento oscilador puede acontecer en un plano o incluso en todo el espacio.

ONDAS EN UN MUELLE

Cuando una onda se genera lo que sucede es que la energía de la perturbación que la ha generado se transmite de unas partículas a sus vecinas en una determinada dirección. Pero las partículas, una vez pasada la onda, se mantienen en su posición original. Por lo tanto, en una onda se transmite la energía, pero no la materia.

GENERACIÓN DE ONDAS

Una onda, sea del tipo que sea, se genera siempre como consecuencia de una perturbación. Una perturbación es una acción producida por un agente externo que rompe el equilibrio del sistema. En el vídeo el sistema es el recipiente con agua y el agente externo es el bastón. Cada vez que el bastón golpea al agua en un punto dado genera una perturbación cuya propagación constituye el frente de ondas.

Así que ya sabes, ya sea que hablemos de ondas en el agua, ondas de sonido, ondas sísmicas o incluso ondas de pensamiento, detrás de todas ellas siempre tenemos una perturbación; ya sea ésta el golpeteo del bastón, un relámpago rompiendo en el aire, el colapso de una falla o la impresión de una fuerte emoción.